| 7.3 – Method to handle Pressure-velocity coupling (SIMPLEC) | ||
Before we start to describe the method used in CFD Studio, we remark that the physical mechanism should be noticed on the development of algorithms in order to deal with this coupling. The correct solution of a momentum transport problem will be obtained provided that the pressures field introduced in the Navier-Stokes equations generates velocities that satisfy the continuity equation. When we are developing an algorithm, properly feedback of the process is essential in order to obtain a good rate of convergence. In the case of coupling, mass residue, calculated using continuity equation is the fundamental datum in order to indicate in which manner the new pressures field should be updated. In the meanwhile this new pressures field should, together with the most recent velocities, satisfies the motion equations. There are several ways of adjusting these variables during the iterative process until we obtain the problem’s solution, when all conservation equations involved will be satisfied. The coupling method used by CFD Studio and described in this method is called SIMPLEC, known also by SIMPLE Consistent. SIMPLE are the initials for Semi IMPlicit Linked Equations. SIMPLEC is based on Chorin’s method [1] and it has as procedure writing the pressure as the sum of the best available estimative for pressure P*and a correction P’ which is evaluated in such a way to satisfy the continuity equation. So we have: |
||
| (7.3.1) | ||
After the pressure field evaluation, we calculate the momentum conservation equations, and it is necessary to correct the velocities in order to satisfy the mass equation. Therefore, we must find the velocity correction equation, and the refinement of these corrections influences considerably the rate of convergence of the iterative cycle. Then, the pressures are updated to complete the cycle. In the SIMPLEC method the equations needed to correct the velocities are obtained from the motion equations. Now if we attribute to Eq. (4.9) the pressure terms |
||
 |
(7.3.2) |
|
 |
(7.3.3) |
|
If we introduce a pressure field P* in (7.3.2) and (7.3.3), we find: |
||
 |
(7.3.6a) |
|
 |
(7.3.6b) |
|
Now, when we insert the appropriate pressure field in (7.3.2) and (7.3.3), then subtracting from these equations (7.3.4) and (7.3.5), considering coefficients and source terms constants, observing that the operator [L] is the pressure gradient numerically approximated, we have: |
||
 |
(7.3.4) |
|
 |
(7.3.5) |
|
| Adding |
||
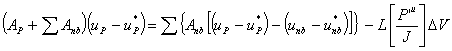 |
(7.3.7a) |
|
 |
(7.3.7b) |
|
| And if the terms in braces are disregarded, we obtain the equations to velocity correction: | ||
 |
(7.3.8a) |
|
 |
(7.3.8b) |
|
As we have stated before, method SIMPLEC is similar to SIMPLEC, and the difference between them is that in SIMPLEC the denominator of the correction velocities equations is given only by AP, this condition imposes the use of severe under relaxation in order to reach convergence. Now, if we insert (4.15) in (7.3.6), we have: |
||
 |
(7.3.9a) |
|
 |
(7.3.9b) |
|
And |
||
 |
(7.3.10) |
|
We should emphasize that Now, we have got to find out an equation in order to determine P' such that when substituted in (7.3.9), it generates velocities u and v which must satisfy the mass equation. We will begin this procedure writing down (7.3.9) at the interfaces of our elemental volume. East face: |
||
(7.3.11a) |
||
(7.3.11b) |
||
West Face: |
||
(7.3.12a) |
||
(7.3.12b) |
||
North Face: |
||
(7.3.13a) |
||
(7.3.13b) |
||
South Face: |
||
(7.3.14a) |
||
(7.3.14b) |
||
- At North and South faces pressures gradients in h direction were disregarded and the terms |
||
(7.3.15a) |
||
(7.3.15b) |
||
(7.3.15c) |
||
(7.3.15d) |
||
It is important to observe that those simplifications do not change the quality in our solutions. We may assert this because the solutions of our problems don't depend in the correction equations, these equations are auxiliaries and don't belong to the system that is being solved. The influence of the correction equations is on the rate of convergence. For this reason the correction equations presented here arise from the equations that we want to solve. Now we must evaluate the contravariant velocities at the interfaces, and substituting (7.3.11) to (7.3.14) into (3.2) and (3.3), we have: |
||
(7.3.16a) |
||
 |
(7.3.16b) |
|
(7.3.16c) |
||
(7.3.16d) |
||
Then after some algebraic tricks in (7.3.16), we have the contravariant velocity equations, which given by: |
||
(7.3.17a) |
||
(7.3.17b) |
||
(7.3.17c) |
||
(7.3.17d) |
||
a and g are components of the metric tensor of (3.4) e (3.5). Finally, in order to find our desired equation, we substitute (7.3.17) in mass equation: |
||
(7.3.18) |
||
So we get a Poisson equation for P’: |
||
(7.3.19) |
||
And the coefficients are given by: |
||
(7.3.20a) |
||
(7.3.20b) |
||
(7.3.20c) |
||
(7.3.20d) |
||
| And | ||
(7.3.21) |
||
As we obtained P', the contravariant velocities Ue, Uw, Vn e Vs are corrected by (7.3.17), and the correction of the Cartesian velocities in the center of elemental volumes may be done in two ways: First: Evaluate the velocities directly from (7.3.9). Second: Evaluate the contravariant velocities in the center of the elemental volumes, using the corrected contravariant velocities of the faces, as in the following equations: |
||
(7.3.23a) |
||
(7.3.22b) |
||
And: |
||
Uc = contravariant velocity normal to x, and constant in center of the volume Vc = contravariant velocity normal to h, and constant in center of the volume |
||
As we have the contravariant velocities in the center of the elemental volume, we can calculate the Cartesians velocities using the inverse of (3.2) and (3.3), we have: |
||
(7.3.23a) |
||
(7.3.23b) |
||
After these updates we have, therefore, a velocity field that satisfies the mass equation, and in the next step the pressure P is obtained from (7.3.1). In the new iteration P’ is attributed to the new P and a new velocity field is evaluated. This process continues till we reach convergence according to the specified parameters. We shall study the iterative cycle in details in chapter (10). Soon, we will see that (7.3.1) does not have a physical foundation. This equation is neither obtained from mass equation nor from momentum equation. This procedure is only a simple way to advance the values of P in time. P’ has an important physical interpretation in the velocity correction equations, but it has not in (7.3.1). |
||
|
||
| << Back | Index | Next >> |
| © SINMEC/EMC/UFSC, 2001. | All rights reserved. |